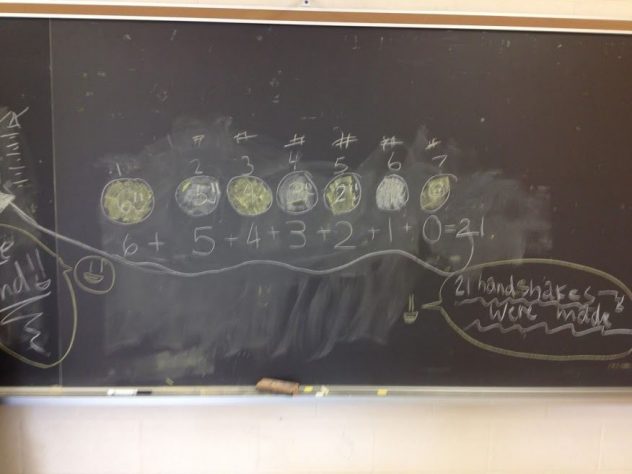By Matthew Oldridge (Father, TEDx speaker, mathematics educator, and thinker.)
When I was first thinking about mathematics as a critical and creative endeavour, I wrote this piece for The Learning Exchange (Ontario Ministry of Education) blog.
It is upsetting that kids don’t see mathematics as a creative, living and vibrant subject. (Some don’t, at least.) Why is creativity only allowed in art class, or music class, or Language Arts class?
My definition of creativity is this:
Making something new.
If pushed, I would flesh out my definition by saying: “making something new with available tools.” To the painter, different types of paints, and papers, brushes, or canvasses are the tools. We can learn to paint, and once we know how to paint, our repertoire will expand, and we can truly make something new.
I never argue for untutored creativity in the math classroom. In the math classroom, we are going to use our basic toolkit to help us “make something new”. We need to know how to use the operations, and we need to build knowledge and skill with fractions, integers, and a number of other things. We must know where “the box” is, and work “inside the box”, to later work “outside the box”. Many mathematics problems have their own constraints, but in using those constraints, we can still come up with interesting and creative solutions to problems.
Consider this problem, which I have used with probably 10 different classes over the years:
10 people are meeting for the first time. They all shake hands with each other, by way of introducing themselves. How many handshakes will happen?
Here is some student’s boardwork about this problem, for six handshakes. Her explanation was so interesting. You can’t really tell by the picture, but it showed serious insight. That’s why we need to listen to and hear kids’ ideas.
This mathematical problem could be about combinations, or using the pigeonhole principle. It could be about “discovering” the structure for the summing of consecutive numbers. We can work with kids to generalize the structure, depending on their age. We might have a specific curricular reason for using this problem. We might not—we might just be looking at kids’ interesting ways of thinking about the problem.
Here is another problem, made famous by Martin Gardner, called the Mutilated Chessboard. I previously wrote, in a blog post for the Ontario Ministry of Education, that creative thinking in mathematics classrooms is “making something new”. In this case, the mutilating of the chessboard (removing the corners), turns something familiar, that 8 x 8 chessboard, into something new- a 62 square odd shape. Changing the familiar to the unfamiliar, and forcing kids “outside the square”, to change a common phrase, is a good way of getting kids to think creatively.
This picture represents one solution. A group found that, no matter how you tile it, two squares of one colour are left. This led to the insight that tiling the 62 square chessboard is impossible.
The thing I have found is that kids have subtle and interesting ways of thinking about problems. In answering the problem, students actively employ imagination and subtle shades of creativity come out. The transition from thinking mathematically, to explaining their thinking out loud often leads to some “magic”. Subtle shades of solution paths will come out, and it is those often subtle differences that are to be celebrated. Creativity is not often a “bolt from the blue”, or a eureka moment. It can be, but often it’s just subtle variations on a solution path.
We are not talking pure, unfettered “splash the paint on the page” Jackson Pollock creativity here, but we are talking about subtle and unique shades of imaginative thinking about the problem. You could think about it like painters choosing different pigments or slightly different shades of the same colour.
Once in awhile, a kid will come up with a radically divergent problem path. This happens often in thinking classrooms. A kid will have a “eureka” moment and see something a new way. This is the “je ne sais quoi” moment of creativity, the magical moment of insight that happens when we, as is our human birthright, think deeply about interesting problems. These moments are to be celebrated. We are no less capable of creative insight in mathematics classrooms than we are in art classrooms.
Creativity in math classrooms is using the tools of mathematics to create new things. Creativity in math classrooms is bringing our thinking to life, using the tools of representation of mathematics.
Mathematics is a creative subject. It’s a living, breathing, creative and vibrant subject.
If we are open to kids’ thinking in math classrooms, we will see and hear those subtle shades and variations that I am calling creative thinking in the math classroom. I hope we are all open to it. A math problem is an empty canvas—give kids mathematical tools and skills, and see how they fill it with their thinking.
Click here for more posts on imaginative math and science teaching.
Enjoying this site?
Subscribe to get a weekly email with our updates. Imagination in learning PreK-Higher Education. All curricula. All learners.