By Fred Harwood (in a Math Coach role for a Grade 6-7 Math Club, @HarMath)
My Teaching Background: I am known predominantly as a secondary mathematics educator. I took one year of teacher training after a BSc in Physics. I was hired 40 years ago to teach Science, Socials, Math and English (yes there were utility roles back then). I was needed mostly as a mathematics teacher at the junior high I started in and did teach some science 8 and 9 classes ten years into my career. My training as an amateur astronomer and physics major gave me some skill sets and attitudes of observation and reflection that greatly aided my growth as an educator. Seeing my teaching career as a calling also gave me a boldness to explore, innovate, adopt, adapt, and create. I have taught many gifted/talented classes throughout my career, which were rich environments for exploration and experimentation. Strengthened by the knowledge that the students were swift and capable learners, they could ‘catch up’ should an experimental lesson go sideways. It was my first modified class of the weakest students in the school that led to my greatest growth as an educator. Struggling math learners lead educators to try different approaches; we must look for a new road to success because the traditional ones do not work for these learners. Like universal design, I soon discovered the ideas learned in the two extreme classes worked just great for the students in regular classes.
Current Setting: I have been volunteering as an outside Math Coach for an upper intermediate math club at an elementary school in British Columbia for the last two years. There are approximately 12 students in the group. Most are in grades 6 and 7 but there is also one quiet girl in grade 5 who just loves mathematics.
My initial goals were for students to realize numbers could be composed and decomposed leading to multiple representations and that their mathematics should speak of their approaches. Reasoning and communicating clearly are essential for building mathematical understanding.
Math Club: September 21, 2016
Here were the students’ challenges:
- Which of the following problems has the largest product? Try to figure it out by solving as few problems as possible. How did you choose which problems to do or not do?
42 x 65 24 x 77 52 x 34
40 x 91 50 x 61 43 x 49
25 x 82 12 x 68 72 x 44
Explain why you think it is the largest.
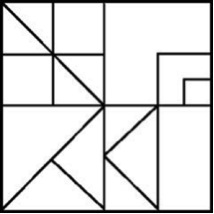
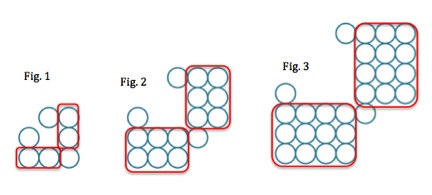
- If the big square is ‘1’, write in how big each region of the shape is and be prepared to explain why you think this:
3. Figure 1 Figure 2 Figure 3
a) What would Figure 4 look like?
b) How many small squares would be in Figure 10? Explain/show how you know?
c) Generalize the pattern into a rule to predict any figure’s shape and the total of the small squares?
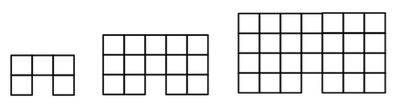
4. What questions might be posed about the following visual pattern?
Fig. 1 Fig. 2 Fig. 3 Fig. 4
What Happened
The students worked away at the first problem but were more interested in the answer than the approaches and reasoning that would reduce the amount of calculations needed. I could see some of their reasoning as I watched them work but even when I drew attention to how one student crossed out the ones they knew could not be the largest, they were not that interested in what other students were doing or thinking.
The “fraction talk” question led to more reasoning but was well within their abilities so there was not enough productive struggle. There were five returning students from the previous year and we had done a half dozen of these through the year. The visual patterns were started but we ran out of time to debrief them well.
After that session, I wanted to do some array counting the next week to increase the level of talk.
I explored some of the “cognitive tools” employed in the Imaginative Education approach. I decided to employ two cognitive tools in my next session. I wanted to see if changing the context of the learning and evoking mental imagery with words could increase students’ involvement with some others’ thinking.
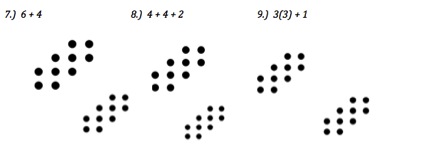
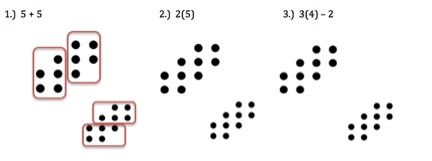
So, instead of having students show how they would count an array of dots, I asked them to imagine how other students counted from their mathematical statements. I also asked them to use words to describe their thinking about the images associated with the arithmetic expressions.
As I listened in on the smaller conversations, I kicked myself for not actually having some of the expressions written in words as it would be mirroring what they were actually saying to each other. E.g. “I saw two sixes but with one corner missing from each” instead of 2(6) – 2. I wonder if that would create a stronger sense of connection between the figures, the verbal descriptions and the spoken words?
These were the questions I gave to my students:
Math Club: September 28, 2016
Directions for students: Our goal today is to ‘see’ mathematics and to see it talk to us. You will need to imagine how other students are thinking and ‘show’ what they might have done to count how many dots are in an array:
Now defend your diagrams with others to see if there were multiple ways to do it or if you feel someone else did it better and why.
I saw them looking at each other’s approaches more often than the previous week. I also watched several conversations start up around “Oh, I see how you thought. It is similar to mine but I saw the 5s sideways.”
The second question after array counting was to revisit some of the previous week’s visible patterns.
Directions to students: Solve the following questions about this growing pattern on your whiteboard with your partner. Remember you are trying to ‘show’ how you thought through the problem clearly enough for others to understand your method and the process you did to solve the problems.
Figure 1 Figure 2 Figure 3
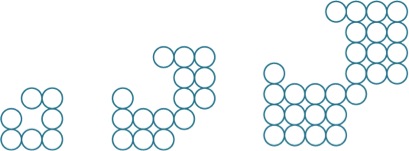
a) What would Figure 4 look like?
b) How many little circles in Figure 6?
c) How many circles in Figure 12?
d) Can you generalize a formula to predict the number of circles in any Figure?
e) If there was a Figure 0, what would it look like and why?
Based on the instructions I provided for this problem, you can see I wanted students to build on their experiences of imagining other students’ communication. More visible patterning questions like these can be found on Fawn Nguyen’s website. These are powerful because they indicate that there are multiple approaches possible and the mathematics created will explain how they think.
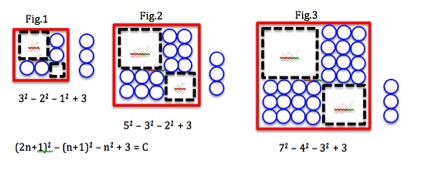
For example, one group solved it this way:
Letting n = the figure number we can see, each red box grows from 1×2 to 2×3 to 3×4 etc.
Circles = 2n(n+1) + 3 because each red box is n(n+1) and there are 2 boxes so 2(n (n+1)). Then there are the 3 circles outside of the red boxes, which are the same for each figure, so they are the constant.
Another group moved the 3 constants out of the way and looked at the remaining pieces as a big square minus two smaller squares like this:
Eureka!
Suddenly, while typing up this blog, an AHA Moment hit me regarding Imaginative Education. I have been showing an example of how thinking with an Imaginative Education approach in mind led me to try something differently—and I had positive results.
My realization: I was a product of the tenets of Imaginative Education. My own life story offers an argument for adopting this approach in all classes. (Stay tuned!)